Value Inversion in Computer Graphics
When dealing with different kinds of images and datasets in computer graphics, specifically compositing, one of the most important concepts to master is that of value inversion. It is the flipping of numbers around a defined pivot, reversing the order of ascension/descension. Whether you’re inverting an alpha matte for a holdout or flipping a positive noise pattern into the negative domain to use as subtractive displacement, it’s vital to understand the maths behind the buttons and the nodes in different softwares to truly be in control of the results.
I’m going to discuss three methods of inversion, how they work and which situations to use them in.
Complement Invert: Pivoting From 0.5
(1-x)
The most common inversion in CG packages and the default “Invert” node inside Nuke is 1-x. When you run this expression over every pixel in an image, you’re going to invert it pivoting from 0.5. Black becomes white, mid-grey stays the same (being the pivot) and white becomes black. This is usually used when dealing with alpha mattes such as keys, roto mattes and holdouts that have been scaled or clamped to fit between 0 and 1.
Houdini
Nuke
Take the example below of x=0.2. To flip this, 1–0.2 would give 0.8. x=0.5 though would resolve 0.5, proving the pivot.
This method causes problems however when you have values outside of your normalized range, as super-white positives and negatives will flip into the opposite domain, often leaving your image either blown out or burnt with negative values.
Booleans
It is though great for flipping booleans, such as the result of an if statement. Inside Nuke for example, ‘Grade1.disable’ would resolve a “0” if called with the node turned off. However if you wanted to link that up to a check box in a gui to enable/disable, it might be counter-intutive to turn something off when you tick the box, so you’d want the inverse result. Therefore ‘1-Grade1.disable’ would give you the opposite result and checking the box would turn on the node.
Modifiying Ramps
When you have an array of linear values ascending or descending in an image plotted between 0 and 1, complement inversion will losslessly flip it back and forth. You can use this to your advantage for example when dealing with a key or roto matte. In the example below you may want to isolate just the edge pixels in an “edge detect” fashion.
This result is achieved through (x*(1-x))*4, where x is your image channel r, g, b or a. The fourth image describes the new slope of the gradient which started as a linear curve.
The results of both 0*1 and 1*0 are both 0, meaning that the high end of the gradient is reduced to 0. However 0.5*0.5 results in 0.25, meaning that we end up with a slope from 0 to 0.25 and back to 0 again. To normalize the central peak to 1, simply divide 1 by 0.25 to get your reciprocal (which is 4), then multiply your gradient with that.
Alternatives
You can also use a custom variable in the place of the “1” in 1-x to offset the pivot, which will let you tailor the response you get. This is an alternative to pre/post-offsetting your image if it doesn’t fit in the 0–1 bounds, however it isn’t perfect.
Additive Inverse: Pivoting From 0
(x*-1)
This can be just as useful a method of inverting images and maps as the complement invert, however it serves a distinct other purpose. The formula x*-1 pivots from 0, rather than 0.5. This means it is perfectly suited for flipping positive and negative numbers interchangably, with the added advantage of not being constrained to normalized ranges. A value of any size could be inverted this way and it would flip to the opposite domain — this is great for working with vector maps which distort or displace geomtery or images based on their magnitude and vector. A positive number * -1 will always be negative, however a negative number *-1 (negative*negative) will always be positive.
sin(x)
sin(x)*-1
Both images show the same sine wave plotted from -1 to +1, with baseline 0 running through the centre. The second graph has inverted the wave and what was once a positive peak is now a negative valley.
Displacement
When working with displacement the key attribute of your map besides the strength of the value is whether it lies in positive or negative space. This will define whether you’re displacing your geometry inwards or outwards. In the example images below, I have a data map driving displacement which in the first one exists only in the positive domain, between 0 and 1.
Positive
Negative
In the second image, I’ve flipped the map by multiplying by -1, this then displaces the surface internally.
Negative Values in Footage
Frequently with under-exposed footage, negative values can crop up which can cause problems down the line in compositing. Merge maths stops working correctly and spatial filters go bezerk, so it’s an important thing to watch out for. To be clear, negative values are not a bad thing. They can simply be a symptom of your colourspace not having the range to contain them. You might find that negative values in one space are not present when you convert to another space. This is why clamping negatives is not a good idea, as you might remove them and then find further down the pipeline when the footage is converted to another space, you’re missing data (this is a good argument for working in the largest space possible, such as ACES, before scaling down for delivery). If you really need to get rid of them, you can potentially do a toe lift or subtle offset.
You can use additive inversion to check for negatives.
Multiplicative Inverse
(1/x) or (x^-1)
The multiplicative inverse is the number which when multiplied by x, equals 1. The expression for finding this value is 1/x. In imaging we can use this as a tool to map all values above 0 inversely on a non-linear scale, distributing low values gradually on the high end and high values exponentially tighter together on the low end. It is well suited for inverting non-normalized images, as superwhite values don’t cause issues. The only caveat is that any pure black values will not compute properly as there is no possible multiplicative inverse of 0 — Nuke will throw up an inf value. Just build an if statement into the expression to assign 0 as 0.0001, or pre-offset your image with that value for example.
To achieve the same mathmatical result, you can also raise to the power of -1, such as pow(r,-1).
To adjust the scale of the inverted output image, replace the 1 with a variable. This can be controlled per channel to change the colour response. This is especially useful for inverting photo negatives and balancing the positive image back to the correct hue.
The below example shows the multiplicative inverse of a linear ramp graphed using 0.036 as the scaling factor, as a value of 1 would exceed the chart. Notice the non-linear weighting of whites to darks in the second image.
Inverting Photo Negatives
In regard to photo negatives, conventional wisdom points to using a complement expression of (1-x) to flip the values around, and then to crunch the black and white points to restore contrast and to finally do some shadow/highlight treatment to add some further micro-contrast into the image and expand the range. However this is not a sound way of converting logarithmic values (which is how light is captured on film) to linear. The following examples show a potentially quicker and more accurate route to perceptually linear results.
Below is a demonstration of the multiplicative inverse vs. the complement inverse of a scanned film negative, flipping it back to positive and balancing tones and colour. Notice the difference in highlight response and the finer graduations visible in the multiplicative inverse result. The curves show the per-channel adjustments done to create the balanced first image.
1/x
1-x
Multiplicative Invert
Complement Invert
After balancing the first image using 0.036/x (with some blackpoint/whitepoint and gamma adjustment), I then matched the second (1-x) to it as closely as possible. Without plotting custom points on a lookup or using any highlight or midtone controls, the closest I could get using blackpoint/whitepoint/lift/gain/offset/gamma was an image that, despite having the same overall colour balance and exposure, lacks a distinct range in the highlights as well as some vibrance in the high end. Inspecting the curves shows the exponential nature of 1/x vs. the result of 1-x. You can also see the converging colour curves which describe the lack of vibrance.
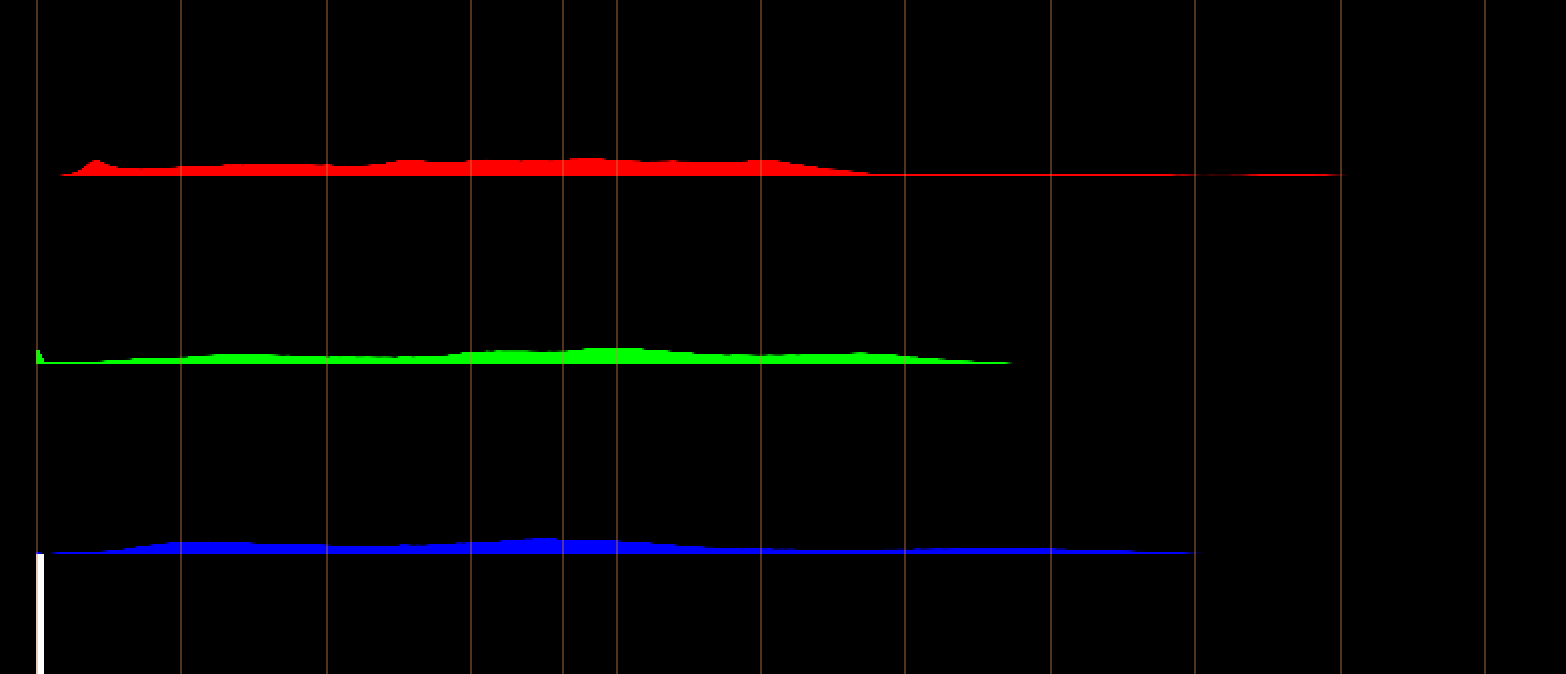
Below the lookups are the histograms for both images — again you see can the wider range in one over the other, with the first image plotting values much further into the high end without bringing the rest of the image with it (which is something that I struggled to match with the second, even with highlight and midtone qualifiers).
The explanation for these results is in the film medium itself. The film response to light is logarithmic, meaning that the relationship between recorded density to light intensity is non-linear. When it comes to inverting a logarithmic negative therefore, we aren’t just inverting an image, we are converting colourspace as well, and we must use exponentiation for that. Using a subtractive invert (1-x) is not going to restore the curve to the linear slope that we would expect to see, which is why lift/gamma/gain failed. However by dividing 1 or a custom variable by our image (which is identical to raising to the power of -1), we pseudo reverse the log scale into something resembling a linear image. It’s not an exact reversal of log (for example it doesn’t raise the value of the natural logarithm to x as a conversion from Cineon to linear space would) but the exponential quality gives similar results in this case.
Using the Reciprocal
The nature of dividing 1/x gives us the value by which to multiply to reach 1. This can be used for reversing certain maths, for example gamma. Gamma correction (raising to the power) is vital to many aspects of imaging, importantly colourspace and compression. A display device might apply a gamma of 2.2 to an image, which means that in order for that image to display correctly, it must be encoded with the inverse gamma prior to display. 1/2.2=0.45, meaning that a gamma-encoded image using 0.45 would display correctly on a diplay using a gamma of 2.2.